Un problema de optimización consiste en: maximizar o minimizar una función objetivo, es decir, obtener el valor máximo o mínimo de una función dada una variable.
En el mundo de la computación se busca resolver los problemas de forma óptima, utilizando la menor cantidad de recursos, con algoritmos eficientes y rápidos.
Problemas continuos y combinatorios
Existen dos tipos de problemas de optimización:
-
Continuos: estos problemas son los que pueden ser resueltos tomando un rango de valores, comúnmente utilizando los números reales, esta característica los distingue de la optimización discreta (combinatoria) ya que en ese caso las variables son restringidas y pueden ser binarias.
-
Combinatorios: estos problemas son difíciles de resolver, por lo que se recurre a explorar solamente un espacio de soluciones en lugar de todas las soluciones posibles, de esta manera se reduce el espacio de búsqueda y así se resuelven de forma eficiente.
Problemas P y NP
Recordando la definición de un algoritmo, sabemos que es un procedimiento finito que se sigue paso a paso para dar solución a un problema, recibiendo una entrada y devolviendo una salida satisfactoria. La complejidad computacional de un algoritmo, es medida en base al tiempo de ejecución que tarda en llevar a cabo cada paso hasta obtener un resultado, esta es mejor expresada como el número total de operaciones realizadas para obtener la solución.
Un algoritmo es polinomial (P) cuando su tiempo de ejecución está acotado por un polinomio dependiente del tamaño de la entrada. Por lo que un problema es de clase P si tiene solución en un tiempo polinómico por una máquina de Turing determinista, entonces se consideran problemas factibles para resolver de forma eficiente. La familia de problemas P pertenecen a los de optimización continuos.
Algunos ejemplos de problemas de clase P son:
- Ordenamiento por selección
- Algoritmos matemáticos (logaritmos, lineales, cuadráticos o cúbicos)
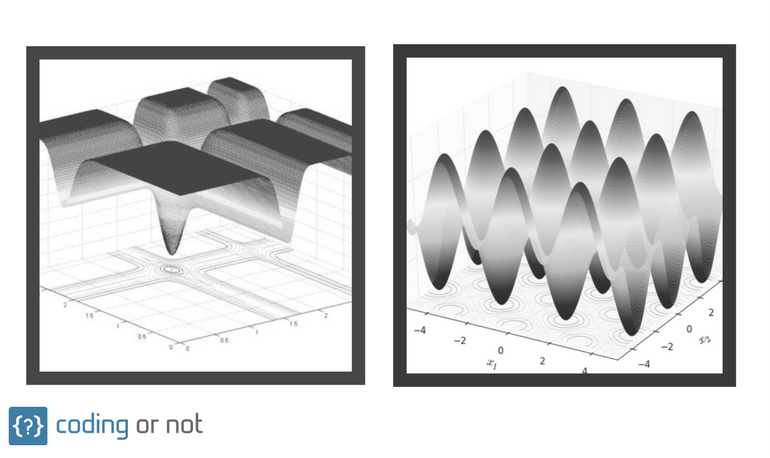
- La función esfera
- La función de Langermann
- La función de Michalewicz
- Las seis jorobas de camello
- Algoritmo de Dijkstra
Un algoritmo polinomial no determinista (NP), es aquel que no se ejecuta en un tiempo polinomial, por lo que dado un problema de clase NP no se conoce un algoritmo que sea capaz de dar solución en un tiempo polinomial. Estos problemas solo pueden ser resueltos encontrando las soluciones de forma aleatoria, para dar con la mejor solución posible. Estos solo pueden ser resueltos en un tiempo polinomial utilizando una máquina de Turing no determinista. Además existe una subclase dentro de los NP conocida como NP-Completo de los cuales si se puede demostrar que uno de ellos es resoluble en tiempo polinomial, entonces también cualquier problema en esta subclase es resoluble en ese tiempo, estos problemas son conocidos como los más complicados de resolver, dado que no se ha podido demostrar que existe dicha solución en tiempo polinomial, así que los problemas NP-Completos no pueden ser resueltos con algoritmos eficientes. Para este tipo de problemas se utilizan algoritmos heurísticos y evolutivos, que si bien, no garantizan que se encontrará la solución óptima, por lo menos encontrarán buenas soluciones en tiempos aceptables. La familia de problemas NP pertenecen a los de optimización combinatorios.
Algunos ejemplos de algoritmos de clase NP son:
- Asignación cuadrática
- Camino hamiltoniano
- Conjunto independiente
- Coloración mínima
- Empaquetamiento (Bin Packing Problem)
- Cubrimiento de vértices
- Agente viajero
- Clan máximo
- Corte máximo
- Satisfacibilidad
- Problema de la mochila
- Cuadros mágicos
- Sudoku
- Aprendizaje de perceptrones multicapa
- Problema de las n-reinas

Espero que esta nota te haya sido útil y que a partir de ahora puedas distinguir a qué grupo pertenece un problema, de esa forma podrás decidir la mejor opción para la implementación de su solución. Recuerda que tus comentarios son bienvenidos.


Muy bien explicado!
¡Gracias por leernos!
Bien explicado!!
Hola
Me alegra saberlo.
¡Saludos!