Un autómata es un modelo matemático para una máquina de estado finito, en el que dada una entrada de símbolos, «salta» mediante una serie de estados de acuerdo a una función de transición (que puede ser expresada como una tabla). Esta función de transición indica a qué estado cambiar dados el estado actual y el símbolo leído.
Simbología de la representación gráfica
Autómata finito determinista
Es un autómata finito que además es un sistema determinista; es decir, para cada estado en que se encuentre el autómata, y con cualquier símbolo del alfabeto leído, existe siempre no más de una transición posible desde ese estado y con ese símbolo.
Ejemplo
Autómata finito que podría formar parte de un analizador léxico. El trabajo de este autómata consiste en reconocer la palabra coding, por lo que necesita siete estados, representando cada uno de ellos la posición que dentro de dicha palabra se haya leído hasta el momento.
Estas posiciones corresponden con los prefijos de la palabra, desde la cadena de caracteres vacía (es decir, cuando no contiene ningún carácter) hasta la palabra completa.
Autómata finito no determinista
Es un autómata finito que, a diferencia de los autómatas finitos deterministas, posee al menos un estado, en el que para un símbolo del alfabeto, existe más de una transición posible.
Definición formal de autómata finito
Sea M un conjunto:
M = (E, A, T, e0, F) donde
- E todos los estados.
- A es el alfabeto de entrada.
- q0 representa el estado inicia que pertenece al conjunto E.
- F los estados finales que están contenidos en E.
- T la función de transición que está dada por: T: E x A -> P(E) donde P(E) es el conjunto de subconjuntos de E.
Cuando se construye la tabla de transición:
T(e,a) = R significa que si se está en un estado e y se lee un símbolo a puede cambiar a cualquiera de los estados e’ que pertenecen a R.
Relación de lenguajes y autómatas
Formalmente, dado un autómata finito no determinista
M = (E, A, T, e0, F) el lenguaje aceptado por M es L(M) definido como
L(M)= {w | existe una computación aceptadora de M con entrada de w}
para el cual se cumplen los siguientes teoremas:
Dado un autómata finito no determinista (AFnD) M, existe un autómata finito determinista (AFD) M’ tal que L(M) = L(M’).
Construcción de gramáticas a partir de autómatas dados y de forma inversa.
Un lenguaje A es regular si existe un autómata finito determinista M con A = L(M).
Un lenguaje A es irregular si existe un Autómata finito no determinista N con A = L(N).
Aplicaciones
- Software para diseñar y probar el comportamiento de circuitos digitales.
- El “analizador léxico” de un compilador típico, es decir, el componente del compilador que separa el texto de entrada en unidades lógicas, tal como identificadores, palabras clave y signos de puntuación.
- Software para explorar cuerpos de texto largos, como colecciones de páginas web, o para determinar el número de apariciones de palabras, frases u otros patrones comúnmente conocidos como expresiones regulares.
- Software para verificar sistemas de todo tipo que tengan un número finito de estados diferentes, tales como protocolos de comunicaciones o protocolos para el intercambio seguro de información.
Resolución de problema
Determinar si un texto de entrada es una dirección de correo válida.
Posibles entradas:
- lorem ipsum dolor
- usuario@servidor.com.mx
- usuario@.com
- usuario@serv&vidor.com.
- @servidor.com.mx
¿Cómo se decide?
codigornot@gmail.com es un correo válido, pues contiene un usuario, seguido de un @, y finaliza con un servidor. Definamos estas reglas formalmente.
Definiendo el alfabeto
El alfabeto puede modelarse con clases de caracteres, en lugar de los símbolos como tal. Dados los caracteres que puede representar una computadora, encontramos las siguientes clases:
- Alfanuméricos : { a,b, …, z, A, B, …, Z, 0, 1, …, 9, _ }
- Arroba: { @ }
- Punto: { . }
- Otros: { todos los demás }
Una vez clasificados los caracteres, nombramos cada categoría:
- Alfanuméricos: w
- Arroba: a
- Punto: p
- Otros: o
Entonces nuestro alfabeto es: S = { w, a, p, o }
Criterios de aceptación
- El usuario debe ser una cadena de caracteres alfanuméricos solamente.
- Seguido de una y solo una arroba.
- El servidor debe ser también una cadena de caracteres alfa numéricos.
- El separador de dominio es un punto.
- El nombre de dominio es una cadena alfanumérica.
- La parte de dominio aparece al menos una vez y puede repetirse.
- Una cadena vacía no se acepta como alfanumérica.
Los estados
Estado inicial:
- No se ha leído nada, se espera el nombre del usuario.
Estados de transición:
- Se está leyendo el nombre del usuario.
- Se ha leído @, se espera el nombre de servidor.
- Se está leyendo el nombre del servidor.
- Se ha leído un punto, se espera el nombre de dominio.
Estado final:
- Se está leyendo el nombre de dominio.
Estado de rechazo:
- Se ha recibido una entrada inesperada.
Cada estado se denota por:
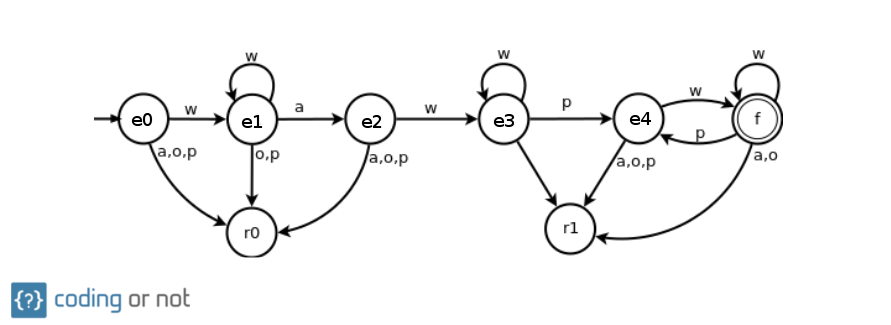
(e0)No se ha leído nada, se espera el nombre del usuario.(e1)Se está leyendo el nombre del usuario.(e2)Se ha leído @, se espera el nombre de servidor.(e3)Se está leyendo el nombre del servidor.(e4)Se ha leído un punto, se espera el nombre de dominio.(f)Se está leyendo el nombre de dominio.(r0, r1)Se ha recibido una entrada inesperada.
Formalmente
- A = {w, a, p, o}
- E = {e0, e1, e2 ,e3, e4, f, r0, r1}
- F = {f}, F está contenido en E
- T: E x A -> E
Vista gráfica del autómata
Función de transición del autómata
|
T
|
e0
|
e1
|
e2
|
e3
|
e4
|
f
|
|
w
|
e1
|
e1
|
e3
|
e3
|
f
|
f
|
|
a
|
r0
|
e2
|
r0
|
r1
|
r1
|
r1
|
|
p
|
r0
|
r0
|
r0
|
e4
|
r1
|
e4
|
|
o
|
r0
|
r0
|
r0
|
r0
|
r1
|
r1
|
Gramática regular
- CORREO: USUARIO SERVIDOR DOMINIO
- USUARIO: w+
- SERVIDOR: aw+
- DOMINIO: (pw+)+
- CORREO: C
- USUARIO: U
- SERVIDOR: S
- DOMINIO: D
Con:
- w: caracter alfanumérico
- a: arroba (@)
- p: punto (.)
Sea
G = {
N = { C, U, S, D }
T = { w, a, p }
P = { C -> USD, U -> w+, S -> aw+, D -> (pw+)+}
f0 = { C }
}
Referencias
- Autómatas finitos no deterministas (AFnD).
- Introducción a la teoría de autómatas y lenguajes formales. Gómez, Meza, Argote, Ibarra. ISBN: 978-607-8104-60-4
- Matemáticas discretas. Richard Johnsonbaug. Sexta edición.
- Teoría de autómatas, lenguajes y computación. John E. Hopcroft, 2007.




Excelente artículo, perfecto para aprender y recordar conceptos muy importantes.
Gracias por tu comentario y por leernos.
¡Saludos!
Excelente articulo, muy gradecido por tan valioso aporte a la teoria de autómata. Saludos desde Venezuela – Caracas
Me alegra que te haya sido útil.
¡Saludos!
pesima la pagina
Hola
Nos puedes dar más retroalimentación respecto a tu comentario, para que podamos seguir mejorando.
Gracias.
si
muy buena información!!
Hola Gamaliel
Me alegra que te haya sido útil ¡Saludos!
hola. muy interesante la informacion
Me esta costando comprender este tema 🙁